K-近邻算法实践：Glass Classification - Kaggle Datasets

可从GitHub(Glass Classification)下载本文源码以及样本数据集

前言

本文主要目的是通过 KNN 也就是 k-近邻算法 来实现一个Glass Classiciation，文中使用的数据来自 Kaggle Datasets ,可以从该页面下载这份数据文件，也可以直接从我 Github 上下载源代码，源代码包括了本文所有内容。 k-近邻算法是 Machine Learning 的一个入门级算法，具备有效性以及易学习。在文章中，我希望通过强调 k-近邻算法 的基本理论，以及如何使用距离测量的方法来进行分类，理论部分的内容十分重要，这关乎到你是否能够理解在面对什么样的数据时可以采用 KNN ，而什么时候又不是那么的适合。

简单来说，k-近邻算法采用测量不同特征值之间的距离，来对数据进行分类。这个距离的计算也是十分简单的，如果你不知道什么是 欧式距离公式 (也有人称它为欧几里得度量法)，那么建议先去了解一下，它是比较简单易懂的。另外代码实现部分，将会使用Python，所以前提要求是你需要学会最基本的Python语法。如果你不懂Python——互联网上有非常多关于 Python 的教程，个人建议可以看看 廖雪峰的Python教学 ， 如果有人认为这个是广告，请联系一下廖雪峰让他支付一下广告费。：)

k-近邻算法
优点	具有较高的精度，且对异常值不敏感、无数据输入假定
缺点	计算复杂度较高（即计算效率并不是那么理想），空间复杂度高
适用	数值型数据以及标称型数据

上表对 KNN 的优缺点以及适用范围进行了简单的描述，当前若没有直观的印象，可以在接下来的内容中，逐一去理解，我会尽量将所有可能存在的疑问，以及实现的每一个步骤都描述清楚。如果文章中的描述有所纰漏，希望能够及时指出，我的邮箱地址为：linyu@szkingdom.com，不甚感激。

k - 近邻算法概述

我们现在先假设存在某数据集合 Datasets ，将其视为样本。这个样本数据集合中每一个数据都存在一个标签，换句话说，我们能够知道这个样本数据集中的每一数据，与所属分类的一个对应关系是什么。当我们输入没有进行标记的数据时，将新数据的每个特征与样本数据集中数据对应的特征进行比较，然后通过算法提取出在这个样本数据集中，特征最为相似的数据（近邻数据）的分类标签。在一般情况下，只需要提取样本数据集中 k 个近邻数据，通常不会大于20个，那么在 k 个数据中出现最多的标签，即是新数据的标签。

举一个简单的例子来理解上面这段话的描述。详见下表样本数据集的表示，即通过一部电影中出现的打斗镜头，以及接吻镜头，为其指定标签为动作片或爱情片。当输入新的数据，打斗镜头有18个，接吻镜头有90个，通过算法我们来计算这个新输入的电影，应该是哪一种类型。

电影名称(数据)	打斗镜头(数据)	接吻镜头(数据)	电影类型(标签)
California Man	3	104	爱情片
He’s Not Really into Dudes	2	100	爱情片
Beautiful Woman	1	81	爱情片
Kevin Longblade	101	10	动作片
Robo Slayer 3000	99	5	动作片
Amped II	98	2	动作片
?	18	90	未确认

通过欧式距离公式我们计算出新电影数据距离样本数据的距离（这里先不纠结于怎么计算出来的，随后我会进行详细解释）

电影名称(数据)	与新数据的距离
California Man	20.5
He’s Not Really into Dudes	18.7
Beautiful Woman	19.2
Kevin Longblade	115.3
Robo Slayer 3000	117.4
Amped II	118.9

在这个距离表中我们能够很直观的找到与新数据距离最近的几部电影，假设 k = 3（意思为找出3个距离最近），那么就是 He’s Not Really into Dudes 、 Beautiful Woman 以及 California Man 这三部电影。

电影名称(数据)	打斗镜头(数据)	接吻镜头(数据)	电影类型(标签)
He’s Not Really into Dudes	2	100	爱情片
Beautiful Woman	1	81	爱情片
California Man	3	104	爱情片

我们在 k 这个集中找出出现最多的电影类型(标签)，决定新数据的电影类型。显而易见，这里的三部电影都为爱情片，因此我们判定输入的新数据是一部爱情电影。

KNN的具体实现流程：

1. 数据收集：可以自己记录数据并设定标签，形成样本数据，也可以从一些开放数据网站找到数据
2. 数据准备：计算距离时需要的数值，最好是结构化数据格式
3. 分析数据：可以使用Python的numpy+Matplotlib等，方法不限
4. 测试算法：计算错误率，调整参数
5. 使用算法：输入新数据，通过算法输出结果，运算 KNN 判定输入数据的分类，执行后续业务处理

这个流程中，数据收集步骤在本文开头就已经做好了，即下载我们所需要样本数据集。如果没有下载，现在该准备一下了，接下来我们就进行实际操作。

从文件中解析数据

拿到样本数据集的第一件事情并不是直接开始编写代码，而是先分析确认这个样本数据集中的主要特征。首先打开下载来的Datasets : glass.csv，每个样本数据一行，共有214行，其中包含的主要特征如下：

特征	特征含义
RI	折射率
Na	钠元素
Mg	镁元素
Al	铝元素
Si	硅元素
K	钾元素
Ca	钙元素
Ba	钡元素
Fe	铁元素

其中的 Type 为标签，以 1-7 的数字作为标记，按照数据提供方描述，分别对应的玻璃类型如下：

标签值	玻璃类型
1	建筑窗户浮法玻璃
2	建筑窗户无浮法玻璃
3	汽车浮法玻璃
4	（ 本样本数据集中没有这类型数据 ）
5	容器玻璃
6	餐具玻璃
7	前照灯玻璃

那么现在我们对样本数据已经具备一定的了解了，要做的是输入新的各项特征值，然后能够通过KNN算法进行分类，将新数据标记出1-7的玻璃类型。接下来我们就着重实现，将这些特征数据输入到CNN算法中，构建一个分类器。

将样本数据集转换为NumPy的解析方法

首先我们先将CSV文件中的所有数据（除了第一行，那是表头）复制，然后粘贴到新建的txt文本中并保存为glass.txt，拿txt当作样本数据文件，里面应该只包含如下类似数据

1.51766	13.21	3.69	1.29	72.61	0.57	8.22	0	0	    1
1.51742	13.27	3.62	1.24	73.08	0.55	8.07	0	0	    1
1.51596	12.79	3.61	1.62	72.97	0.64	8.07	0	0.26	1
…………
1.52065	14.36	0	2.02	73.42	0	8.44	1.64	0	7
1.51651	14.38	0	1.94	73.61	0	8.48	1.57	0	7
1.51711	14.23	0	2.08	73.36	0	8.62	1.67	0	7

随即我们创建一个KNN.py的Python模块，并在其中构建一个 file2matrix 函数，这个函数用来处理输入格式，传入文件名字符串，返回样本矩阵以及类标签向量。如果你不了解什么是矩阵，请随后去补充学习这方面的知识。这里仅简单说一下返回的样本矩阵 —— 该矩阵的总行数为样本数据的总行数，即已知的 214 行 ，而列则是 样本数据中的9 个特征，即为9列，所以返回的将会是一个 214 * 9 的矩阵 ；

在写代码之前，导包:

import numpy as np
import matplotlib
import matplotlib.pyplot as plt

file2matrix：

def file2matrix(filename):
    # 读取文本文件数据
    file = open(filename)
    data_array = file.readlines()
    lines_count = len(data_array)
    # 创建NumPy矩阵以及类标签向量
    sample_mat = np.zeros((lines_count, 9))  # 1
    class_label_vector = [] # 2
    index = 0
    # 解析文本数据到列表中
    for line in data_array:
        line = line.strip()
        list_from_line = line.split('\t')
        sample_mat[index, :] = list_from_line[0:9]
        class_label_vector.append(int(list_from_line[-1]))
        index += 1
    return sample_mat, class_label_vector

注释：
#1 - 利用NumPy构建矩阵，np.zeros(矩阵行数，矩阵列数)
#2 - 构建一个array,存放类标签向量

我们可以验证一下获取到的矩阵和类标签向量：

sample_mat,class_label_vector = file2matrix("glass.txt")
print(sample_mat)
print(class_label_vector[:20])  # 输出前20个，输出全部也行，去掉 [:20]

输出结果：

[[ 1.52101 13.64    4.49    ...  8.75     0.       0.     ]
[ 1.51761 13.89     3.6     ...  7.83     0.       0.     ]
[ 1.51618 13.53     3.55    ...  7.78     0.       0.     ]
...
[ 1.52065 14.36     0.      ...  8.44     1.64     0.     ]
[ 1.51651 14.38     0.      ...  8.48     1.57     0.     ]
[ 1.51711 14.23     0.      ...  8.62     1.67     0.     ]]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]

根据输出结果已经却认，现在已经成功的从文本文件中导入了样本数据，并且按照我们想要的格式进行了处理，接下来就需要对些数据的真实含义了，为了能够更直观的浏览，用图形化方式展示一下数据，以便辨识数据模式。

使用Matplotlib创建散点图

在KNN中创建新的函数 data2view ：

def data2view(sample_mat, class_label_vector):
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    ax.scatter(sample_mat[:, 0], sample_mat[:, 4], 2 * np.array(class_label_vector), 2 * np.array(class_label_vector))
    plt.show()

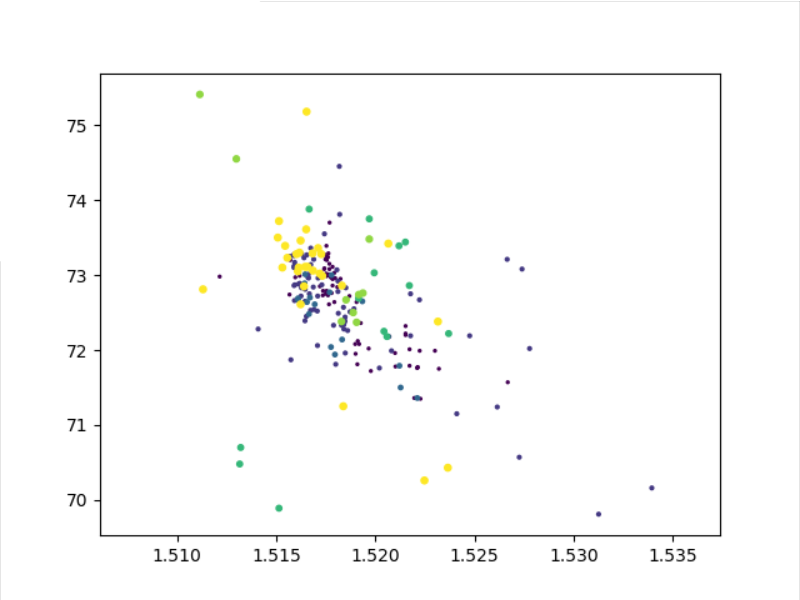
其中的[:, 0]表示为X轴表示从传入的矩阵中取所有行的第一列，第一列所代表的是 RI (折射率)，[:, 4]表示矩阵所有行的第五列，也就是Si（硅元素）。以此类推你可以自己修改这两个参数所取的列数，查看分类在这两个特征值之间的散点分布的情况进行分析。当然Matplotlib除了构建散点图之外还可以构建出其他的图表，你可以通过自己学习Matplotlib来实现，本文重点仅倾向于实现 k-近邻算法。

通过对样本数据的分析不难发现，玻璃的主要构成元素是硅元素，所以散点图是想表示不同分类的玻璃在折射率和硅元素含量这样的一张二维表上的分布情况。

KNN算法的实现

在上一小节中我们构建了一张散点图来分析硅元素和折射率对玻璃分类的一个影响，实际上我们也不需要太过于关于去分析这张图，因为我接下来要说的是如何计算计算两个向量点 xA 和 xB之间的距离，将会用到欧式距离公式：

$$\Large d=\sqrt{(xA_0-xB_0)^2+(xA_1-xB_1)^2}$$

这个公式十分的简单，例如要计算点（1，2）与（3，4）之间的距离：

$$\sqrt{(3-1)^2+(4-2)^2}$$

那么如果数据集存在着多个特征值，则点（1，0，0，1，0）与（2，5，2，3，4）之间的距离计算为：

$$\sqrt{(2-1)^2+(5-0)^2+(2-0)^2+(3-1)^2+(4-0)^2}$$

在此我假设你已经学会了如何使用欧式距离公式，那么接下来我们就该设计一下具体的KNN算法实现，先做一段伪代码，根据伪代码我们还能够理清思路，让真正的代码编写工作变得有条不紊：

对未知类别属性的数据集中的每个点一次执行一下操作：
（1）计算已知类别数据集中的点与当前点之间的距离；
（2）按照距离进行递增排序（即从小到大排序）
（3）选取与当前点距离最近的 k 个点
（4）确定 k 个点中类别的出现频率
（5）返回前 k 个点出现频率最高的类别作为当前点的预测结果

def classify(inX, dataSet, labels, k):
    # 计算距离
    dataset_size = dataSet.shape[0]
    print(np.tile(inX, (dataset_size, 1)))
    diff_mat = np.tile(inX, (dataset_size, 1)) - dataSet
    print(diff_mat)
    sq_diff_mat = diff_mat ** 2
    sq_distances = sq_diff_mat.sum(axis = 1)
    distances = sq_distances ** 0.5
    print(distances)

    # 选择距离最小的k个点
    sorted_distances = distances.argsort()
    class_count = {}
    for i in range(k):
        label = labels[sorted_distances[i]]
        class_count[label] = class_count.get(label, 0) + 1

    # 排序
    sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1),  reverse=True)
    return sorted_class_count[0][0]

'''
使用样本中数据进行一个简单的测试
'''
print("可能分类：", classify([1.52101, 13.64, 4.49, 1.1, 71.78, 0.06, 8.75, 0, 0], sample_mat, class_label_vector, 5))  # 分类:1 ， 返回:1  √
print("可能分类：", classify([1.53125, 10.73, 0, 2.1, 69.81, 0.58, 13.3, 3.15, 0.28], sample_mat, class_label_vector, 5))  # 分类:2 ， 返回:2  √

归一化特征值

从简单的输出测试中我们已经能够看到，似乎是完成了KNN算法。但是这里不得不提出一个问题，让我看来手写一下这个程序中的方程式：

$$\sqrt{(1.53125-1.52101)^2+(10.73-13.64)^2+……+(2.1-1.1)^2+(69.81-71.78)^2+……}$$

应该不难看出，整个公式中，数字差值问题是会影响到计算结果的，在每一组方程计算中，可能都会出现某一特征值过大于其他特征值。我们或许可以这样认为：要对玻璃进行分类，样本数据中玻璃所有构成元素以及折射率应该都是等权重的，不应该出现某一个值过大于其他值，从而照成计算的影响。

那么在处理这样不同取值范围的特征值时，可以采用数值归一化，将取值范围处理为0到1或者-1到1的区间。

$$归一化值 = \frac{输入值-数据集中最小值}{数据集中最大值-数据集中最小值}$$

def norm4knn(dataset):
    min_values = dataset.min(0)
    max_values = dataset.max(0)
    ranges = max_values - min_values
    norm_dataset = np.zeros(np.shape(dataset))
    m = dataset.shape[0]
    norm_dataset = dataset - np.tile(min_values, (m, 1))
    norm_dataset = norm_dataset/np.tile(ranges, (m, 1))
    return norm_dataset, ranges, min_values

# 测试norm4knn
norm_dataset, ranges, min_values = norm4knn(sample_mat)
print(norm_dataset)
print(ranges)
print(min_values)

对算法进行验证

def testing4knn():
    ho_ratio = 0.005
    sample_mat,class_label_vector = file2matrix("glass.txt")
    norm_dataset, ranges, min_values = norm4knn(sample_mat)
    m = norm_dataset.shape[0]
    print('m=',m)
    num_test_vecs = int(m * ho_ratio)
    print(num_test_vecs)
    error_count = 0.0
    for i in range(num_test_vecs):
        classifier_result = classify(norm_dataset[i, :], norm_dataset[num_test_vecs:m, :], class_label_vector[num_test_vecs : m], 5)
        print("分类器分类 : %d, 实际分类 : %d" % (classifier_result, class_label_vector[i]))
        if (classifier_result != class_label_vector[i]):
            error_count += 1.0
    print("分类器分类错误率 : %f" % (error_count / float(num_test_vecs)))

testing4knn()

编写分类预测程序

def classifyGlass():
    resultList = [1, 2, 3, 4, 5, 6, 7]
    inp_ri = float(input("折射率:"))
    inp_na = float(input("Na:"))
    inp_mg = float(input("Mg:"))
    inp_Al = float(input("Al:"))
    inp_Si = float(input("Si:"))
    inp_K = float(input("K:"))
    inp_Ca = float(input("Ca:"))
    inp_Ba = float(input("Ba:"))
    inp_Fe = float(input("Fe:"))
    datingDataMat, datingLabels = file2matrix('glass.txt')
    normMat, ranges, minVals = norm4knn(datingDataMat)
    inArr = np.array([inp_ri, inp_na, inp_mg, inp_Al, inp_Si, inp_K, inp_Ca, inp_Ba, inp_Fe])
    classifierResult = classify((inArr - minVals)/ranges, normMat, datingLabels, 3)
    print("该玻璃分类可能为:", resultList[classifierResult - 1])

classifyGlass()

running & result

折射率:1.52101
Na:13.64
Mg:4.49
Al:1.1
Si:71.78
K:0.06
Ca:8.75
Ba:0
Fe:0
该玻璃分类可能为: 1